
Best Blackjack Odds: Complete Analysis of Blackjack Odds
Blackjack odds are essential to all New Zealanders wishing to up their game performance. Our experts help you to understand and maximise your odds at Blackjack.
What Are Blackjack Odds?
Odds are a probabilistic set of data describing the possible results and their likelihood of occurring in the casino table game.
Knowing the odds of potential winning at Blackjack represents the starting steps to understanding the game thoroughly. It also is how you start playing in an online casino Blackjack, professionally.
What are the Blackjack Odds of Winning?
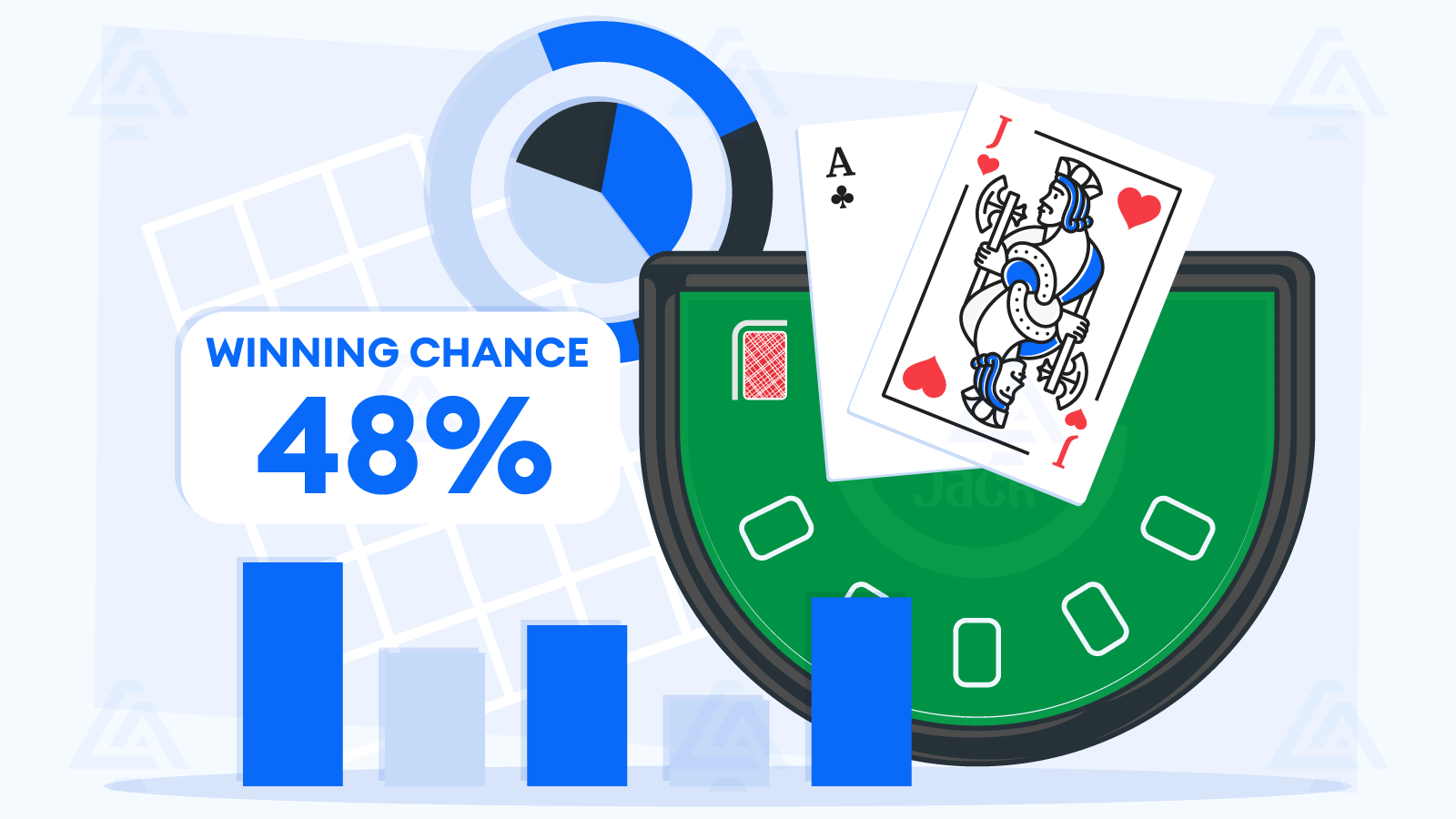
The overall chance of success for your hand against the dealer’s is 48%. The probability means that, at any hand, the chances that you are successful fall marginally short of a fair coin toss.
Naturally, this is a general result. The situation can greatly change depending on your dealt cards, in-game decisions, and the underlying strategy you apply.
In order to maximise your winning chances, trying out a few first-hand tested techniques can be beneficial on the long term. For beginners, the double deck Blackjack strategy can be a good starting point.
What are the Odds Against You?
Another more comprehensive result that presents the game probabilities comes in the form of the house edge.
What is the House Edge of Casino Games?
The theoretical result reflects the profit percentage a casino can expect from any hosted activity across time.
Some online casinos will list the Return to Player rate instead. You should remember that the two are opposites. The RTP shows the percentage returned to the player, while the house edge is the amount kept by the gambling service.
The house edge does not reflect on a round-to-round basis. Rather, it portrays the number of funds you will lose from the wagered total across a statistically relevant number of played hands.
While the standard house edge for casino Blackjack is around 0.12%, if you play the game with basic strategy, it gets reduced to 0.05%.
Which Blackjack Has the Best Odds?
| Blackjack Versions | The House Edge |
|---|---|
| Switch | 0.73% |
| 21 Burn | 0.60% |
| Standard | 0.50% |
| Spanish | 0.42% |
| High Streak | 0.41% |
| Multi-Hand | 0.40% |
| European | 0.40% |
| Bonus | 0.38% |
| Surrender | 0.38% |
| Pontoon | 0.36% |
| Atlantic City | 0.35% |
| Vegas Strip | 0.35% |
| Single Deck | 0.25% |
| Double Deck | 0.23% |
When to surrender
Several players may be curious about what is surrender in Blackjack. Simply put, Blackjack surrender is a rule which allows players to fold their hand, and recover half of their initial wager. Hence, recognizing when the odds are not in your favor may not help you win, but it will indeed help you save some funds.
NZ player’s in-game decisions will affect the Blackjack odds of winning directly and significantly more than any rule variation.
Facts Behind Blackjack Odds
We arrive at the probabilities by considering all the possible outcomes of a decision, then considering the probability distribution between them. This approach is just basic probability theory.
New Zealanders need to keep in mind that no result will ever inscribe the future events of their hand. However, the results do describe the general likelihood of each event occurring.

How Are Blackjack Odds Calculated?
We will start with the basics. Let us calculate the chances for a specific card to come up.
-
The Game Odds for Each Card
To simplify, we will consider a single-deck game version. Blackjack is played with decks containing 52 cards.
Let us choose the card, for instance, the ace of spades. This choice is one among 52 cards in total. Thus, out of 52 possibilities, we want to find the probability for one specific card.
The formula for Calculating Odds
We can use the following formula: Probability = Desired Outcomes / Total Outcomes. Hence, the probability that your first dealt card is an ace of spades is 1/52 or 0.0192 (or 1.92% in percentages.)
However, the colour is unimportant in standard Blackjack. Let us figure out the chances for card values being dealt.
-
The Probability for First Dealt Cards
We will think of the probability that you start the round with a 9-valued first dealt hand. In one deck, four cards have this value. Thus, we have four desired outcomes from a 52 total, which should clarify that the chances are 4/52, or 0.0769 (7.69%.)
Quiz 1: What are the Chances for a Face Card?
All face cards, except for the ace, have a set value of 10. The face cards are the King, the Queen, and the Jack. Each has four colour variations. Thus, the desired outcomes total 12 options out of 52. The probability is 12/52 = 0.23077 = 23.077%.
Quiz 2: How Can You Arrive at the Chances for a First 10-Value Card?
You could count the face cards, along with the 10 number cards and use the same formula. However, you have the probability of a face card coming up, and the chances for any one number card being the first dealt one.
Knowing these stats, you can sum them up and arrive at 0.07692 + 0.23077 = 0.30769.
When calculating the odds of winning at Blackjack, you can replace ‘or’ with summation and ‘and’ with multiplication.
Thus, you are saying that you desire one 10 number card OR any non-ace face card.
First Key Result: The Probability of a Natural Blackjack
This result is important, given the Blackjack 3 to 2 payout for an initial 21-hand. We need to think about what the result we desire is.
Options for a Natural Blackjack
| First Card | Second Card |
|---|---|
| Ace | Face Card |
| Ace | 10 Card |
| Face Card | Ace |
| 10 Card | Ace |
Here, we will want a set value for the first card AND the second one.
For a natural Blackjack
We look for the probability of an ace coming up first and a ten-value card second, or a ten-value card first and an ace second.
Calculate the Odds of Winning at Blackjack with a Natural
- Probability of an ace dealt first: 4/52
- Probability of a 10-value card coming up first: 16/52
- Probability for an ace coming up second: 4/51
- Probability of a 10-value card coming up second: 16/51
For the last two results, we consider that the first card has been dealt. Thus, the remaining pool of occurrences has only 51 possibilities left. Additionally, we consider that the same card has not come up first. Thus, the desired options remain 4 (for aces) or 16 (for 10 and face cards.)
The formula ends up being: 4/52 × 16/51 + 16/52 × 4/51 ≈ 4.826%.
The House Edge Reflects the Game Odds
House edge is a probabilistic result that uses the Blackjack odds of winning and losing and the staked and returned real money amounts. The calculation thus provides the overall money the Blackjack player may expect to lose.
The house edge is the reverse of a game’s return to player rate. We mention this, as the RTP is easier to comprehend for the average gambler.
To arrive at the RTP, you divide the amounts returned to players by the total staked amounts. For the house edge, you just subtract the RTP from 100% (corresponding to a game that returns all staked amounts.)
The Expected Value of Blackjack Games
By expected value, we refer to another probabilistic result that provides the average outcome of an event in the long run.
To calculate it, you figure out all possible outcomes, their probabilities. In the situation of a real money gambling game, also add the stakes and payouts.
Example with Simple Odds of Winning at Blackjack
Let us say that you are playing an odd version of Blackjack. You only win by having a natural 21. The payout will remain the standard 3 to 2. The two possible events are getting a natural Blackjack and winning or losing otherwise. For a £2 wager, you either get back £5 or lose £2.
We have calculated the probability of a natural Blackjack to be ~4.83%. Since we know that there are only two outcomes, the chances of losing are 100% – 4.83% = 95.17%.
The expected value is £5 × 0.0483 + 0.9517 × (-£2) = -£1.6619.
In the long run, you should expect to lose around £1.662 for each round of this incredibly unfair version of the table game.
Blackjack Odds Tables
| Your Current Hand Total | Probability of Busting on Hit |
|---|---|
| 1 to 11 | 0% |
| 12 | 31% |
| 13 | 39% |
| 14 | 56% |
| 15 | 58% |
| 16 | 62% |
| 17 | 69% |
| 18 | 77% |
| 19 | 85% |
| 20 | 92% |
| 21 | 100% |
The game probabilities that you may bust on a hit for each hand do not fully portray the difference between soft and hard hands.
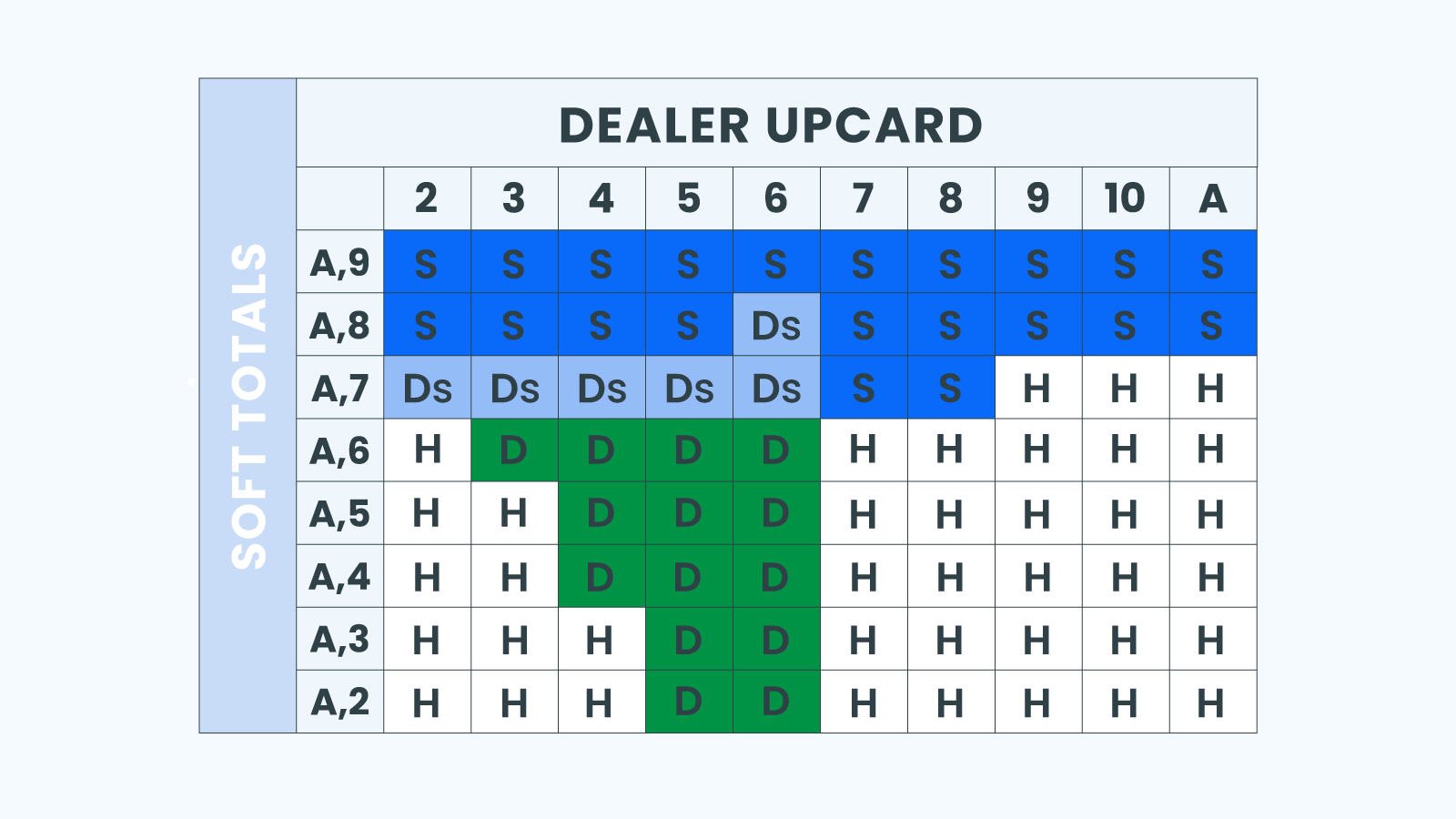
- A soft hand contains one ace that can take both the values of 1 and 11. An ace and a 5 card represent a soft hand.
- You can have two types of hard hands. You either have no ace, or the ace cannot take the value of 11. Here are two examples: A face card, a six, and an ace, or a seven and a face card.
Hard Vs. Soft 16: A Blackjack Odds Table Example
| 16 Hand Types | Chances of Getting the Hand | Chances of Busting on Hit |
|---|---|---|
| Soft | 1.21% | 0% |
| Hard | 6.93% | 61.54% |
This example can help you figure out the odds of busting for any type of hand you hold. We have considered a one-deck option, although the logic applies to multiple decks of cards.
The Blackjack Odds for Busting with a Soft Hand
Soft 16 hands must contain an ace. Thus, the remaining card must be a 5. The probability of having this hand is 2 × (4/52 × 4/51) = 0.0121. Here, the story is simple. No card would lead to a bust since the ace can convert to 1.
The Blackjack Odds for Busting with Hard Hands
| Hard 16 Hands | Odds of Occurrence |
|---|---|
| 6 & 10 or Face Card | 4.82% |
| 7 & 9 Cards | 1.21% |
| Two 8 Cards | 0.90% |
The dealt cards that will lead to a bust for these hands are any, starting from 6 to 10, and the face cards. There is an easier method of arriving at the game chances for a 3rd card bust. We look at the probabilities that your hand will remain under the value of 21 instead.
You will remain in the game if you receive any card, from 2 to 5, or an ace. Thus, there are five groups with four cards each. The probability that you receive any of those is 1/52. The total odds of getting one such card is 5 × 4 × 1/52 = 38.46%.
There is a 38.46% chance that you are in the green on a hit. Therefore, by the same logic as in the case of the house edge, the probability that you bust is 100% – 38.46% = 61.54%.
Bottom Line: Should You Hit for a 16 Hand?
Part of the answer seems evident: you always hit for a soft hand. This decision is correct. However, NZ players may have a more difficult time deciding for hard hands.
It may seem that hitting is simply riskier and, as such, you should not consider it. While this is a correct inference from the previous odds, your decision will depend on another factor.
Your decisions and odds of winning at Blackjack will depend on the dealer’s upcard.
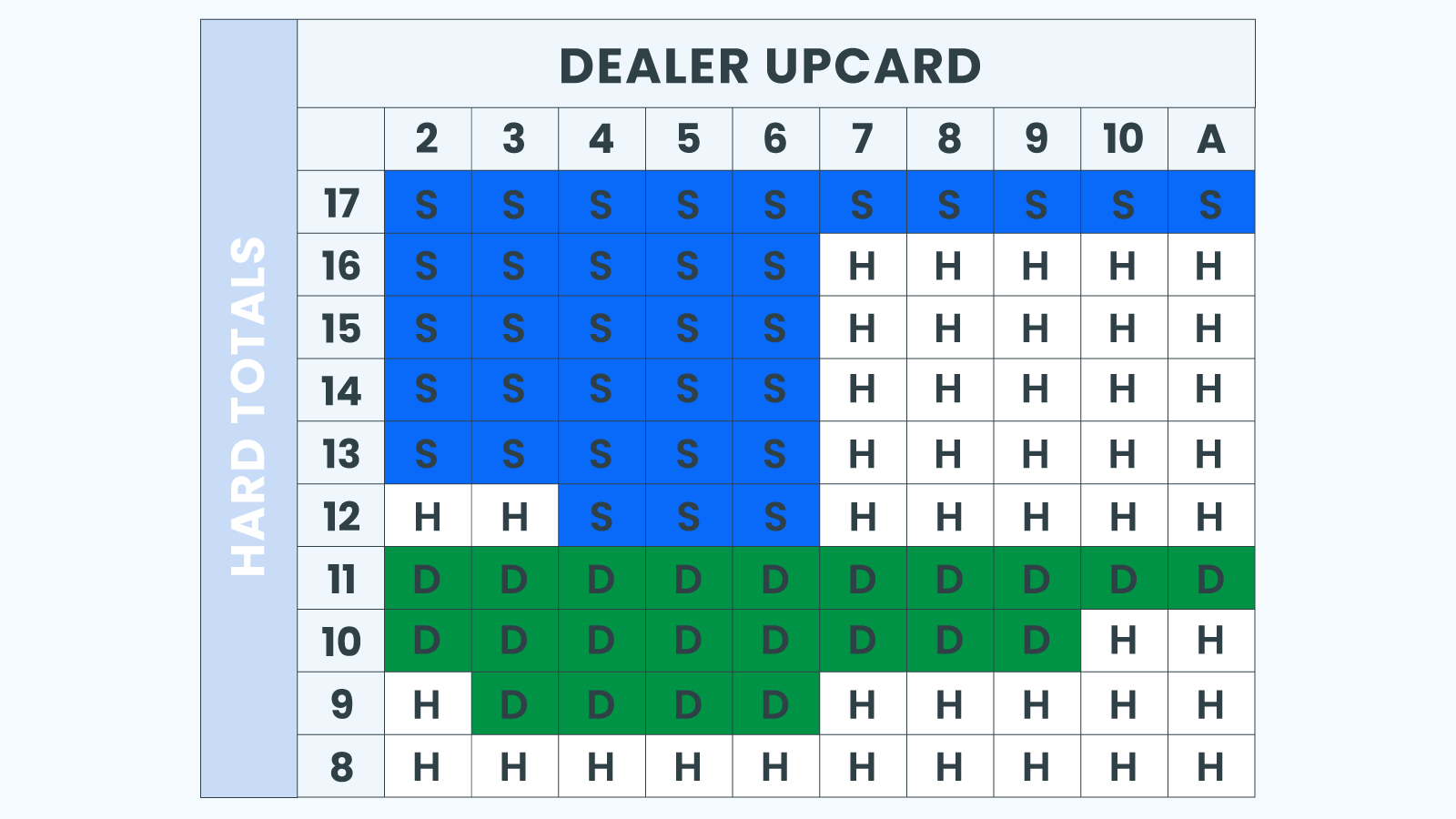
For our examples of the 16 hard hands, you should stand for any upcard from 2 to 6. You should hit for any higher value, including the ace. The calculation behind this result goes beyond our discussion. They are part of the basic strategy for the game.
What Affects the Odds?

Top New Zealand online casinos that players can access will provide multiple Blackjack entries with different rule variations. These outliers will directly affect the house edge and, in turn, your Blackjack odds of winning.
We have provided the overall house advantage for most Blackjack versions available on the NZ market. However, you should understand how each rule changes the edge:
Rule Variation Blackjack Odds Table
| Blackjack Variation | Changes House Edge (with Basic Strategy) |
|---|---|
| Six Decks of Cards | -0.020% |
| Five Decks of Cards | -0.013% |
| Four Decks of Cards | -0.059% |
| Two Decks of Cards | -0.187% |
| One Deck of Cards | -0.463% |
| Dealer Hits on Soft 17 | +0.215% |
| Cannot Double Down After Split | +0.127% |
| Cannot Hit After Splitting Aces | 0 |
| Cannot Re-Split Aces | +0.181% |
| Blackjack Pays out 6 to 5 | +1.358% |
| Can Split 9-11 Cards Only | +0.100% |
| Re-Split to 2 | +0.092% |
| Re-Split to 3 | 0 |
| Re-Split to 4 | -0.017% |
| Late Surrender | -0.076% |
| Lose Initial Bet After Dealer Blackjack | +0.118% |
Now New Zealanders do not need to remember the house advantage for each specific game variation.
Check the table rules and add or subtract the percentages to find the final house edge.
These house rules will affect the Blackjack odds of winning and making sure that you pick a worthwhile video or a live dealer casino. These will either have an informational tab, or the real dealer will inform you of the current rules.
-
The Dealer’s Upcard
The first in-game element that will affect your chances and decisions is the upcard. This is your sole information beyond your dealt cards. The free variable in play will be the possible value of the obscured or hole card.
You may have noticed the hit or stand on soft 17 rule already. But dealers have several regulations they must abide by. Most tables will have them hit on 16, for instance. These rules exist to give players a “fighting chance.”
Do you think the dealer has a Blackjack?
In this case, be rest assured, for not everything is completely lost. If you have the ability to keep evidence of all the 10-valued cards and think you can estimate the remaining ones in the deck, you may try out the Blackjack insurance wager.
Blackjack Odds Table for a Dealer Bust
| Dealer Upcard | Dealer Hits on Soft 17 | Dealer Stands on Soft 17 |
|---|---|---|
| 2 | 36% | 35% |
| 3 | 38% | 37% |
| 4 | 40% | 40% |
| 5 | 42% | 42% |
| 6 | 44% | 42% |
| 7 | 26% | 26% |
| 8 | 24% | 24% |
| 9 | 23% | 23% |
| 10 / Face Card | 23% | 23% |
| Ace | 20% | 17% |
Blackjack Odds with Basic Strategy
NZ players can utilise betting systems that do not require any knowledge of the odds of winning at Blackjack, such as the very simple Martingale Blackjack system. However, these methods cannot replace the basic strategy.
When referring to the basic strategy, gambling experts mean a statistically backed set of decisions that take into account only your cards and the dealer’s upcard.
You have seen how time and mentally taxing Blackjack odds of winning or busting calculations can be. Complexity only increases when you must assess both your hand and the dealer’s upcard and busting possibilities.
Naturally, all gamblers have met this obstacle. For this reason, they devised a compact and comprehensive method of remembering the moves deemed correct by Blackjack odds.
Blackjack Odds Charts
-
Hard Totals
-
Soft Totals
-
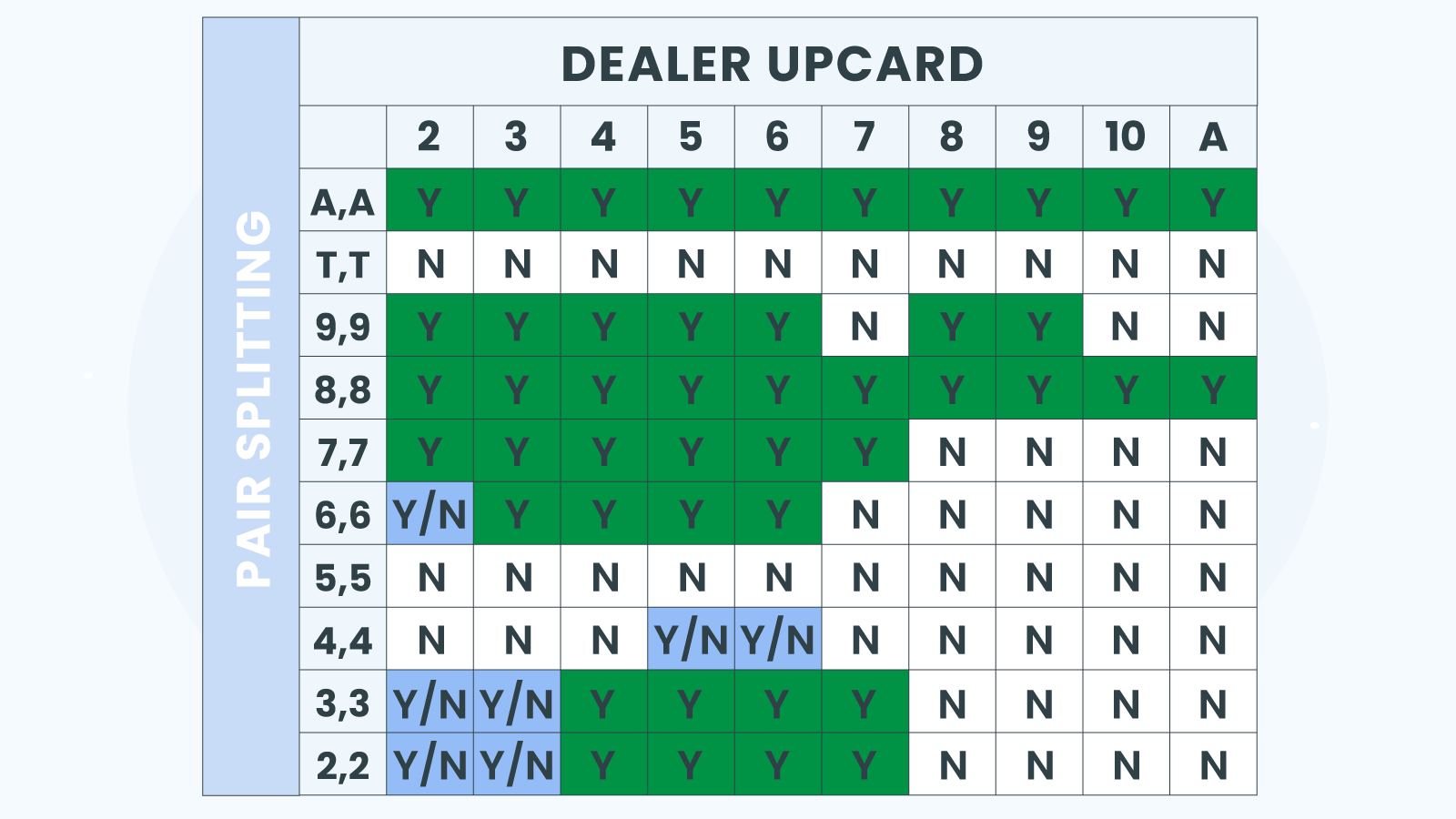
Pair Splits
The Surrender Option, Insurance & Even Bets

Be aware
If the even money stake or insurance bet are available, do not ever take them.
The Blackjack Strategy Goes Further
You will see more than just your hand and the dealer’s upcard when playing at a table. The cards of other players and those previously dealt and removed off the table also affect your Blackjack odds of winning.
The process of remembering them is called card counting. It is as helpful for your cash funds accumulation as it is difficult to master properly.
This strategy is not illegal by any means. Still, land-based casinos will either remove card counters from the tables or utilise disturbance methods.
Card Removal Influence on Odds of Winning at Blackjack
We can portray the varying probability following removed cards by an example. We will consider a four-deck version of the game. We will see how your odds for an initial 21 hand evolve following cards’ removal.
A natural Blackjack requires a 10-value card and an ace. The probability for it with the decks intact is 4.756%. We will consider that you did not get a 21 hand initially, but there was an ace dealt during the round. How will your odds change?
Natural Blackjack Odds Table, Depending on Removed Aces
| Aces Removed | 10 Cards Removed | Total Cards Removed | Natural Blackjack Odds |
|---|---|---|---|
| 0 | 0 | 0 | 4.756% |
| 1 | 0 | 6 | 4.729% |
| 0 | 1 | 6 | 4.965% |
| 1 | 1 | 4 | 4.564% |
| 2 | 1 | 10 | 4.522% |
| 4 | 4 | 20 | 4.096% |
| 8 | 4 | 24 | 2.851% |
| 4 | 8 | 24 | 3.991% |
| 12 | 4 | 30 | 1.523% |
| 4 | 12 | 30 | 3.961% |
| 16 | 0 | 20 | 0% |
| 0 | 64 | 70 | 0% |
The discarded aces have a bigger effect on the natural Blackjack odds. In contrast, any discarded card that is not an Ace or a 10-value card will raise the total odds of having an initial 21 hand.
The effect magnitude of the removed aces grows faster than that of the 10 valued cards. Hence, we see a difference of more than 2% in parallel scenarios for four discarded aces, and 10 removed value cards or 12 discarded aces and four removed 10 valued cards.
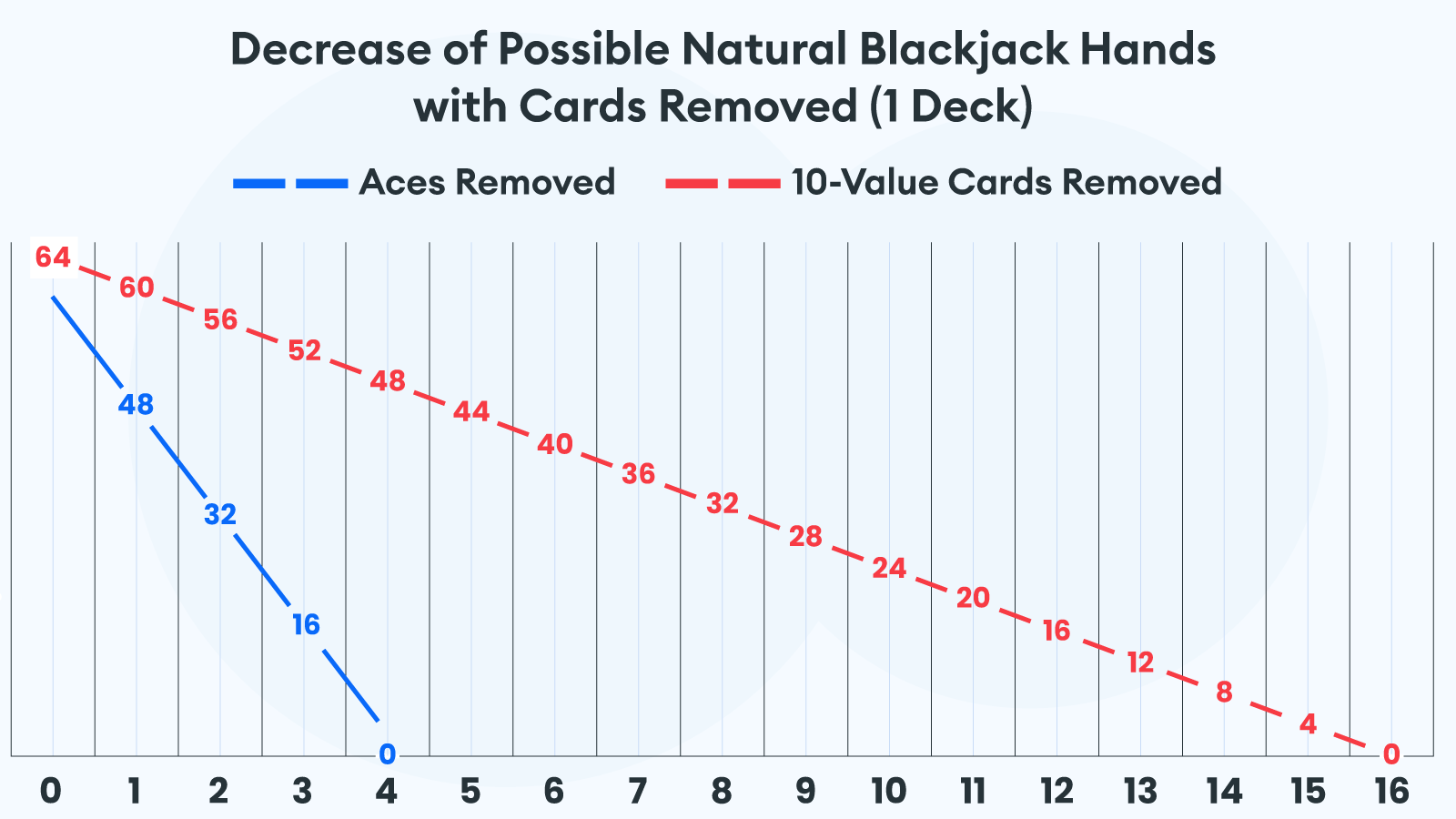
This fact is due to the difference in initial cards in the deck. There are 16 aces and 64 cards having a value of 10. To arrive at a natural Blackjack, you need one ace and one face or 10 cards. When you remove one ace, you eliminate 64 possibilities for such a hand. While, by removing a card with the value of 10 with the aces intact, you only eliminate 16 such options.
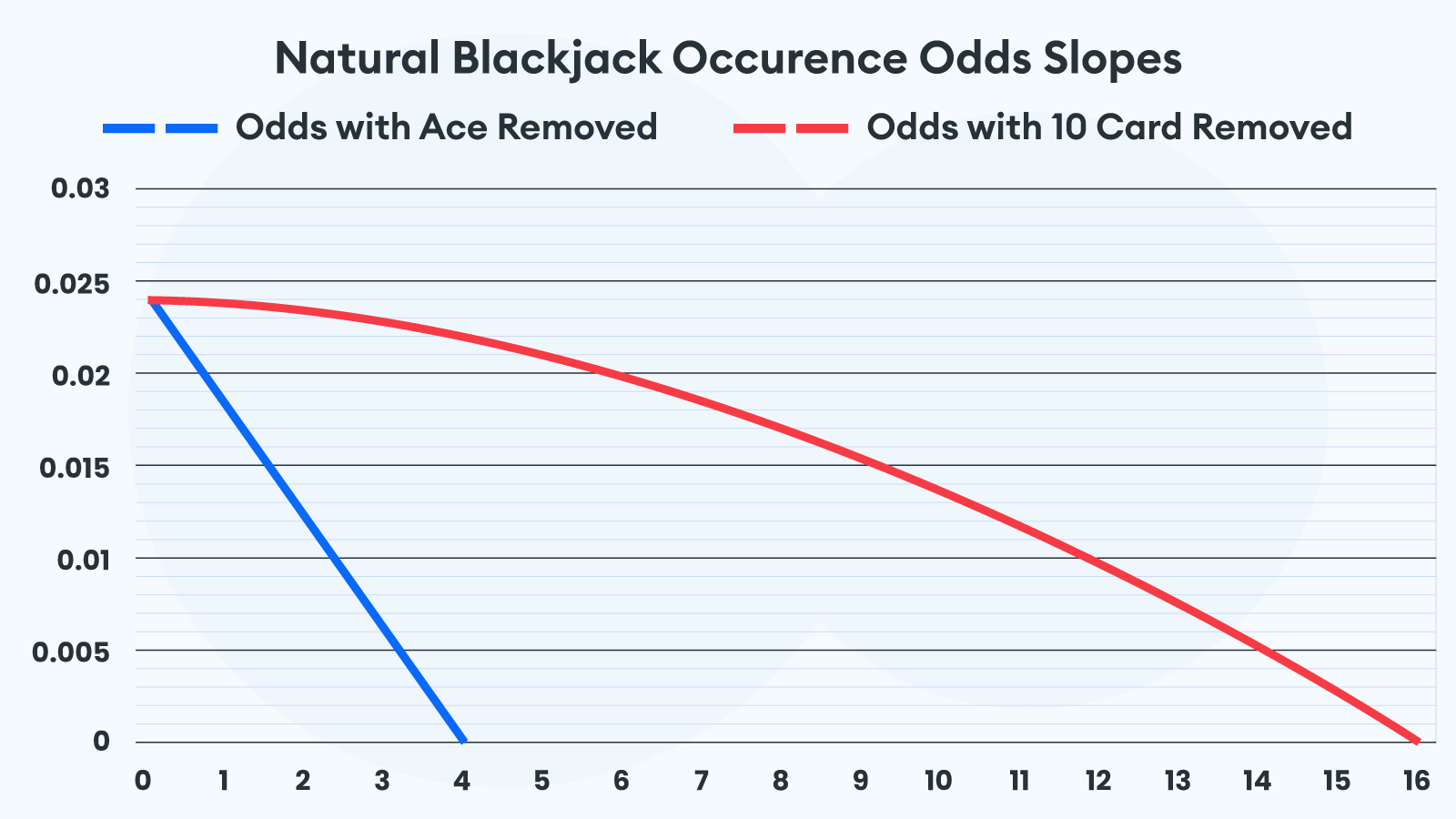
While the combinations decrease linearly when discarding several cards, the odds for a natural 21 valued initial hand do not. Granted, the correlation between removing aces and the probability decrease is much stronger. Still, for the 10-value cards, this is not entirely the case. You can glimpse this fact when combining the two data set representations. The columns correspond to the total natural blackjack combinations, while the lines show the odd evolution.
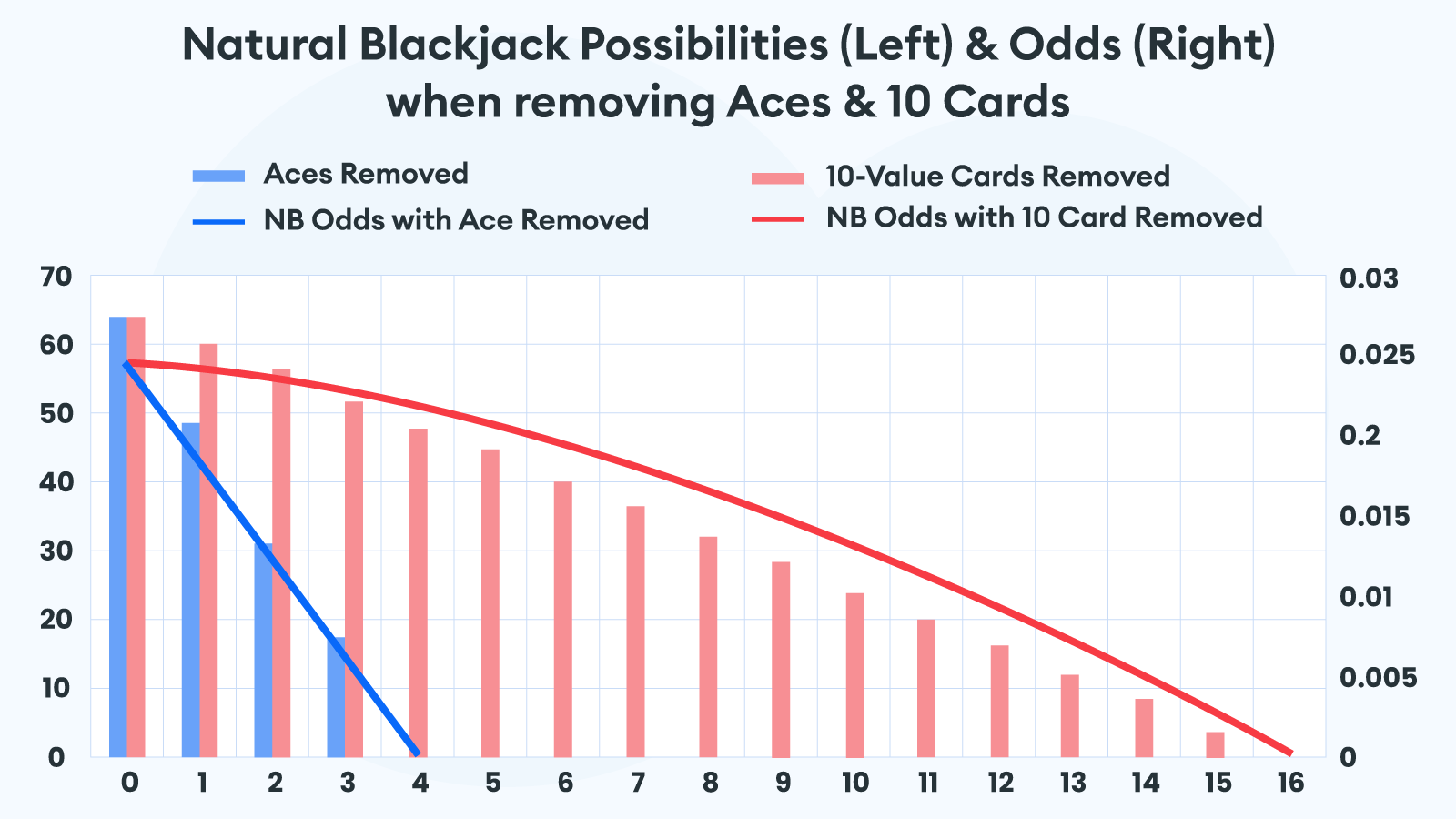
While the blue line for discarded aces closely follows the corresponding columns, the natural odds when removing 10 cards goes to zero at a slower pace. We can conclude that the number of aces in the decks of cards will always represent the dominant variable for an initial 21, while the 10 cards still count but to a lesser degree.
Card Removal Odds Depending on Decks
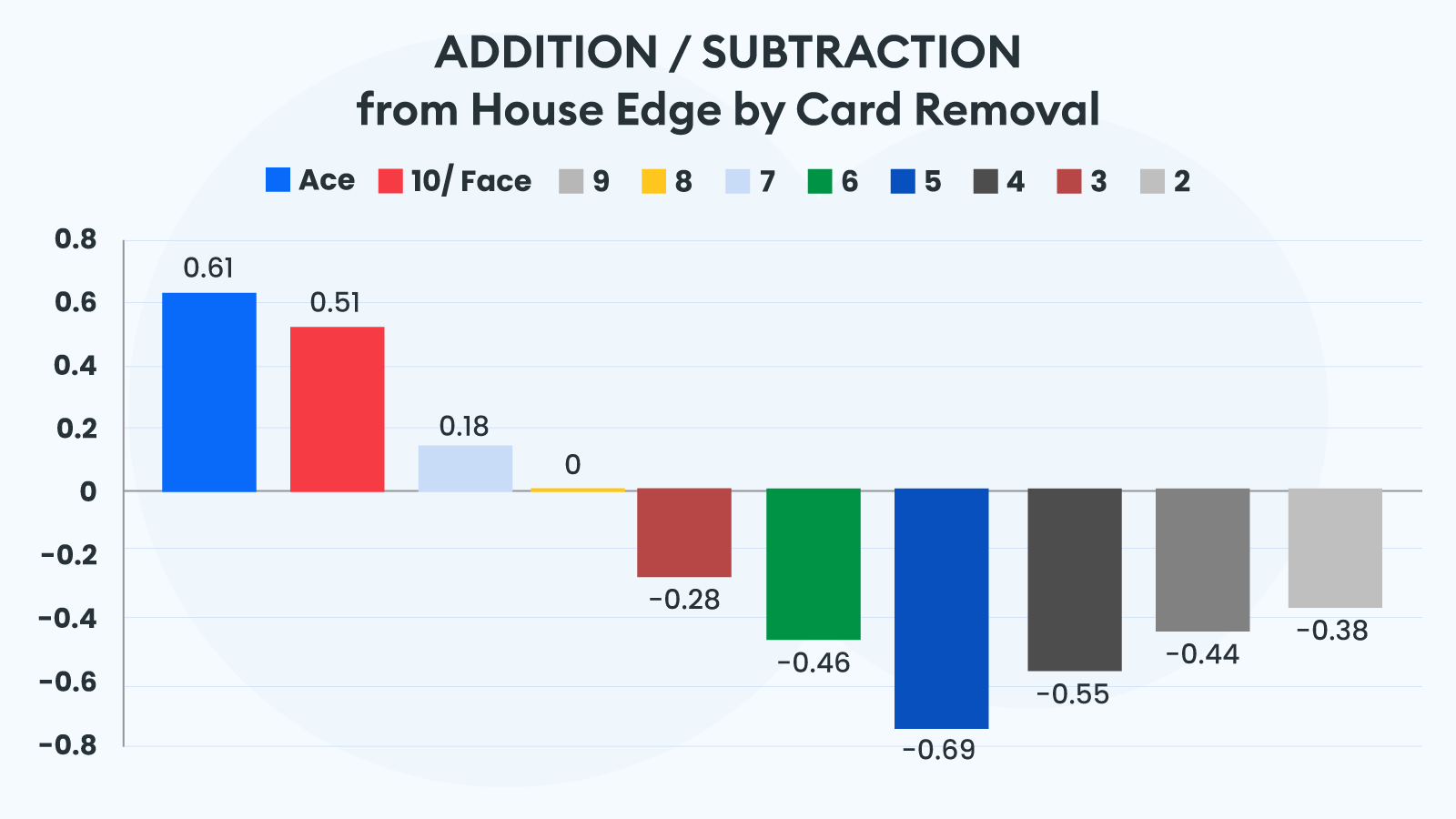
Nevertheless, beyond the probability for a natural 21, all cards’ removal from the game will affect your overall Blackjack odds of earning any payout. The change is better reflected by looking at the house edge in each scenario.
The main lesson from these statistics is that eights are neutrals. Their discarding does not affect your chances in any manner. Any card with a lower value will give you better odds, with 5 cards being the best for removal, while higher-value ones raise the house edge.
The house advantage variation confirms our conclusions from the natural Blackjack example. The most important card type to be attentive to is the ace. Not only does the card play a key role in forming a 21 score, but it also generates soft hands, which provide an advantage to the player.
Card Removal Effects in a Multi-Deck Game
While the number of aces and any other card will be directly proportional to the number of decks in use, their weight in your odds varies. We can portray the property using the same example of a natural Blackjack in any one round.
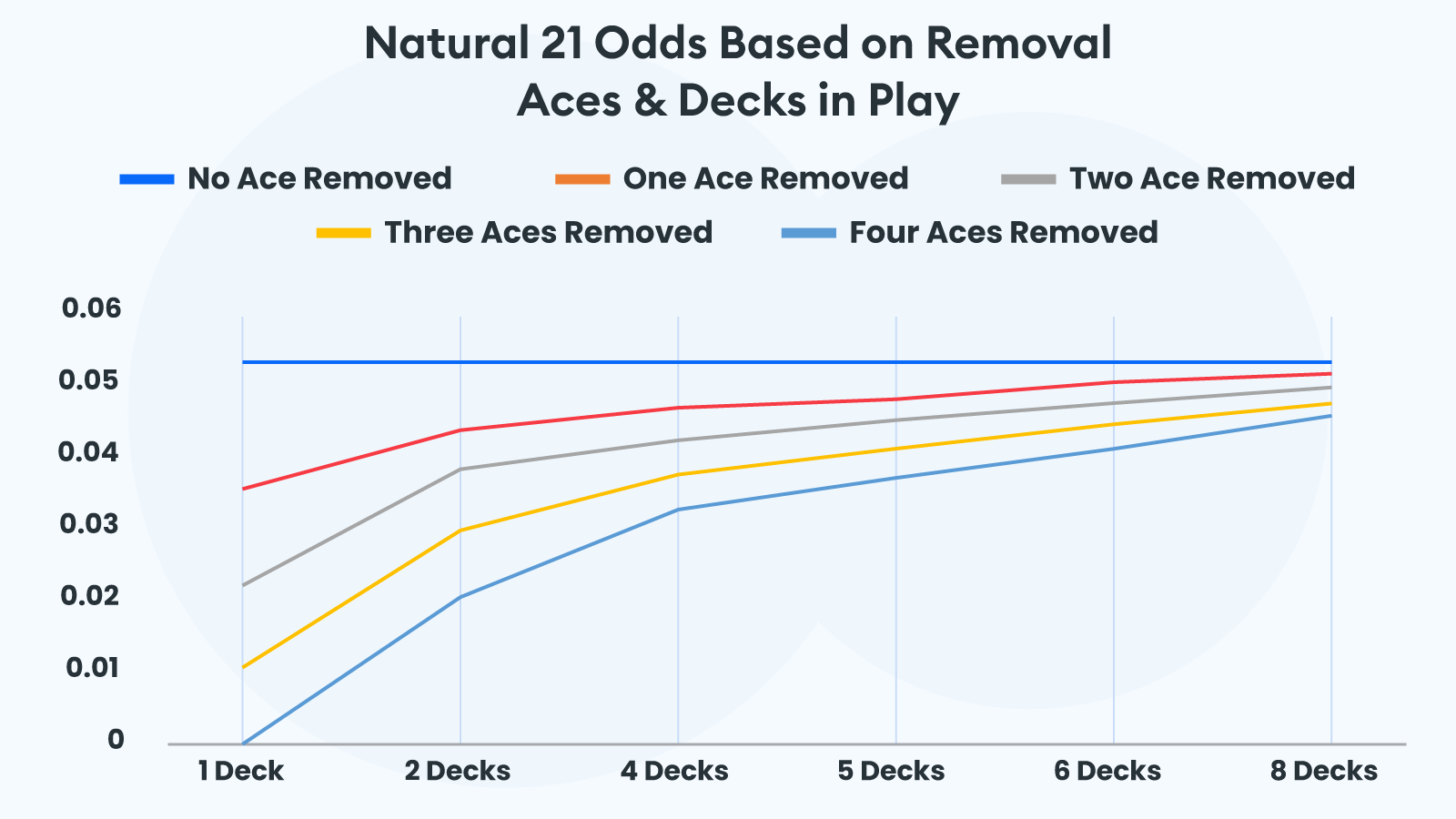
Are Blackjack Odds Better with More Players?
The pure house edge or the one modified by the correct strategy is not affected by the number of players involved in a game. This is the case since the basic strategy only takes your hand and the dealer’s upcard into account.
Thus, your Blackjack odds of winning do not vary based on the number of players at the table. Using the basic strategy is equivalent to imagining playing a game version with infinite decks and even probability distribution for the dealt cards. It only addresses the decisions you should take in each round and based on your present hand.
But we know this is not the case since all tables have a limited number of decks in play and the game odds for certain values being dealt depending on the discarded cards.
Does the Number of Players Matter If You Follow Discarded Cards?
The more cards you can see, the better your approximations are for the modified house edge following cards’ removal. This is the theoretical answer. However, your efforts to keep up to date with dealt hands will also grow accordingly.
You fall under the risk of bogging down in minute calculations that will not necessarily translate into better in-game decisions. Can you effectively find the real-time house edge based on your fellow players’ cards during a round? You have all the tools to do so. However, a 1% or less change in one round cannot inform your betting approach.
Steps to Maximise the Odds
- Understand the odds of winning at Blackjack and basic rules.
- Get a basic understanding of how different game versions will affect the house edge.
- Find the best option of the game and base your choice on verifiable data.
- Understand the background of the basic strategy and its effects on the odds.
- Get familiar with basic strategy chart layouts and try to learn them by heart.
- Step beyond the basic strategy by working out how card removals will affect the game.
- Try paying attention to the dealt and discarded games.
- Integrate this approach into your gameplay and learn when to deviate from the basic strategy.
Now that we’ve simplified the blackjack odds for you, did you see better results in your play?















